АНАЛИЗ ПРЕДПРИЯТИЯ ОНЛАЙН

Корреляционно-регрессионный анализ: «Влияние внутренних и внешних факторов на цену»

Цель: определить влияние внутренних и внешних факторов на цены, то есть изменение цен в зависимости от сезона продаж.

Метод корреляционно регрессионного анализа

В качестве факторов для анализа выбраны:

• - количество упаковок;
• - количество отгруженных единиц;
• - цена продажи;
• - затраты на продажи;
• - скидки с продажи;
• - потери по отсрочке платежа;
• - цены конкурентов;
• - спрос на товар.

Помощь с анализом в практической части ОНЛАЙН ЗДЕСЬ

Используются данные по наиболее распространенному сезонному антивирусному лекарственному средству «Лекарство» (Приложение 1). Для данного товара сезонным является период с октября по март месяцы (в таблице выделено серым цветом), а не сезонными соответственно с апреля по сентябрь.

Приложение 1

Сводная таблица факторов по одному клиенту за период 12 месяцев (октябрь 2018 – сентябрь 2019 г.)

Период, мес.	Цена продажи, руб.	Количество упаковок, шт.	Количество отгруженных единиц, шт.	Затраты на продажи, руб.	Скидки с продаж, руб.	Потери по отсрочке платежа, руб.	Цены конкурентов, руб.	Спрос, руб.
	y	x1	х2	x3	x4	x5	x6	x7
10	146,54	6987,00	1023852,03	5119,26	20477,04	17405,48	143,61	1177429,83
11	159,92	10705,00	1711959,67	8559,80	34239,19	29103,31	156,72	1968753,62
12	161,44	23745,00	3833448,71	19167,24	76668,97	65168,63	158,21	4408466,02
1	148,15	5304,00	785767,40	3928,84	15715,35	13358,05	145,18	903632,51
2	150,54	4455,00	670644,28	3353,22	13412,89	11400,95	147,53	771240,92
3	154,08	18623,00	2869474,85	14347,37	57389,50	48781,07	151,00	3299896,08
4	148,72	1104,00	164181,69	820,91	3283,63	2791,09	145,74	188808,94
5	143,84	1346,00	193614,70	968,07	3872,29	3291,45	140,97	222656,91
6	142,77	259,00	36977,40	184,89	739,55	628,62	139,91	42524,01
7	143,53	237,00	34016,74	170,08	680,33	578,28	140,66	39119,25
8	144,32	595,00	85871,54	429,36	1717,43	1459,82	141,44	98752,27
9	144,83	4575,00	662579,62	3312,90	13251,59	11263,85	141,93	761966,56

Метод: множественный корреляционно-регрессионный анализ по t-критерию Стьюдента (с использованием табличного процессора Microsoft Exsel).

Сущность корреляционно регрессионного анализа

При множественной корреляции изучается зависимость результативного признака от двух или более независимых факторов, что позволяет учесть разнообразные причины, влияющие на результативный показатель, более полно оценить его вариацию. Анализ проводят по примерно той же схеме, что и при изучении парных связей. На первом этапе проводят отбор факторных признаков. Прежде всего путем логического анализа выявляют факторы, которые могут непосредственно воздействовать на результативный показатель. При этом необходимо исключать факторы, которые можно рассчитать на основе других, уже включенных в анализ.

Помощь с анализом в практической части ОНЛАЙН ЗДЕСЬ

Необходимо также учитывать корреляционную зависимость факторов между собой. В идеале они должны быть полностью независимыми; при высокой межфакторной корреляции возникает так называемая мультиколлинеарность, приводящая к искажению коэффициентов регрессии и затрудняющая их интерпретацию. Во избежание такого эффекта производят отсев факторов с помощью таблицы парных коэффициентов корреляции. Если два фактора теснее связаны между собой, чем каждый из них с результативным показателем, один из этих двух факторов исключают из анализа.

Показатели корреляционно регрессионного анализа

Отсев факторов производят также и при оценке значимости коэффициентов регрессии. Важное значение, как и в случае парной корреляции, имеет выбор формы связи. Задача это довольно сложная, поскольку факторы не только влияют на результативный показатель, но и взаимодействуют между собой. В настоящее время вопросы выбора формы связи при множественной корреляции отработаны недостаточно. В большинстве случаев используют уравнение множественной линейной регрессии:

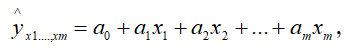
где  - результативный признак;
х1 х2,… хт – факторные признаки;
а0 - точка начала отсчета;
а1 а2, ат - коэффициенты регрессии.

Помощь с анализом в практической части ОНЛАЙН ЗДЕСЬ

Параметры уравнения, как и при парной корреляции, обычно определяют методом наименьших квадратов. Для этого нужно решить систему нормальных уравнений:

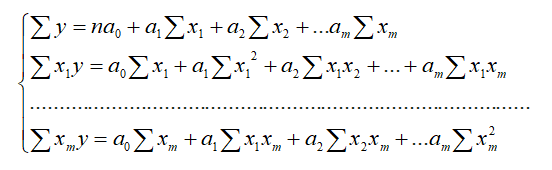
Коэффициенты регрессии множественной связи показывают, на сколько изменится величина результативного показателя при изменении значения фактора на единицу при неизменном значении остальных факторов.

Оценка корреляционно регрессионный анализ

Общая оценка полученного уравнения проводится с помощью индекса корреляции, который при множественной линейной связи называют также коэффициентом множественной корреляции:

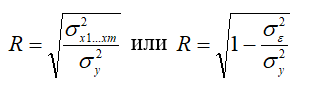
где 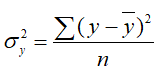 - общая дисперсия результативного признака;

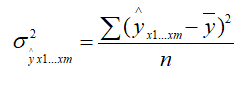- его факторная дисперсия;
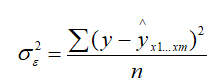- его остаточная дисперсия.

Величина R показывает степень зависимости результативного показателя от всей совокупности факторных признаков. Как и индекс корреляции при парной зависимости, она меняется в пределах от 0 до 1. Квадрат коэффициента множественной корреляции называют коэффициентом множественной детерминации. Он показывает долю общей вариации результативного признака, определяемую совокупным действием факторных признаков.

Помощь с анализом в практической части ОНЛАЙН ЗДЕСЬ

Корреляционный регрессионный анализ примеры

Существенность коэффициента множественной корреляции и всего уравнения регрессии в целом оценивают с помощью F-критерия Фишера или t-критерия Стьюдента. Фактические их значения рассчитывают по формулам:

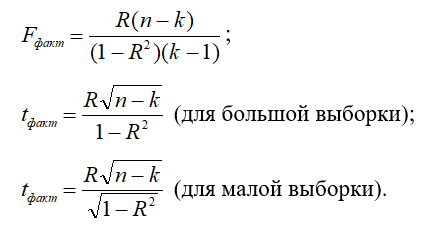
где n - численность выборочной совокупности;

k - число параметров в уравнении регрессии.

Многофакторный корреляционно регрессионный анализ

Полученные значения F-критерия и t-критерия сравнивают с табличными. Число степеней свободы вариации для F-критерия 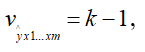, для t-критерия v = n - k. Если фактические значения превышают табличные, связь между признаками считается достоверной, а уравнение регрессии - существенным.
Оценку значимости коэффициентов регрессии проводят с помощью t-критерия по формуле:

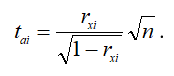
Ее применяют при шаговом регрессионном анализе, когда поочередно отсеивают факторы, имеющие незначимый коэффициент регрессии. При этом первыми отбрасывают факторы, которые имеют наименьшее фактическое значение t-критерия.

Помощь с анализом в практической части ОНЛАЙН ЗДЕСЬ

Задача корреляционного регрессионного анализа

Анализ данных коэффициентов регрессии показывает, что все факторные признаки (x) имеют тесную связь с результативным (y) (Приложение 2). Наибольшая сила связи с результативным у шестого фактора (цены конкурентов – парный коэффициент корреляции равен 1,000). При этом, однако, наблюдается и высокая мультиколлинеарость: большинство факторов имеет достоверную связь друг с другом. Однако сравнение парных коэффициентов корреляции показывает, что только между первым и вторым факторами зависимость (0,999380) выше, чем зависимость между первым и результативным показателем (0,854832). Поэтому первый фактор необходимо исключить из уравнения регрессии.

Приложение 2

Результаты корреляционного анализа

Оценим значимость коэффициентов регрессии с помощью t-критерия (Приложение 3). Наименьшее значение имеют коэффициенты регрессии при факторах х4, х5 и х7. Табличное значение при уровне значимости 0,05 и v = n – k = 12 – 6 = 6 оно составляет 2,4469. Следовательно, коэффициент регрессии при факторах х4, х5 и х7 является несущественным и их следует исключить.

Приложение 3

 

Значение t-критерия Стьюдента при уровнях значимости                                0,10, 0,05 и 0,01

Это означает, что скидки с продаж, потери по отсрочке платежа и спрос не оказывают существенного влияния на цены продаж.

Корреляционно регрессионный анализ факторов

После исключения факторов х4, х5 и х7 получим окончательный результат (Приложение 4).

Теперь коэффициенты регрессии при всех факторах являются существенными, поскольку фактическое значение t-критерия превышает табличное (при уровне значимости 0,05 и v = n – k = 12 – 4 = 8 оно составляет 2,3060). Следовательно факторы х2, х3 и х6 можно включить в уравнение регрессии.

Помощь с анализом в практической части ОНЛАЙН ЗДЕСЬ

Уравнение регрессии значимо, поскольку фактическое значение F-критерия 8564469 превышает табличное (Fтабл = 5,32 при уровне значимости 0,05, v1 = k – 3 = 4 – 3 = 1, v2 =n – k = 12 – 4 = 8). Связь между признаками очень высокая, коэффициент множественной корреляции R = 0,9999. Коэффициент детерминации R2 = 0,9999 показывает, что 99,9% колеблемости продажных цен объясняются включенными в уравнение факторами.

Таким образом, на продажные цены «Лекарствоа» существенное влияние оказывают количество отгруженных единиц, затрат на продажи и уровня цен конкурентов. Так, увеличение отгруженных единиц на 1 единицу снижает цену на 0,005 руб., увеличение затрат на 1 руб., увеличивает цену на 1,002 руб., увеличение цены конкурентов, увеличивает продажную цену на 1,02 руб.

Применение корреляционно регрессионного анализа

Полученное уравнение регрессии позволяет прогнозировать цену на «Лекарство» с учетом сезонности, если известны факторы, ее определяющие.

Приложение 5

Значение F-критерия Фишера при уровне значимости 0,05 (v2 = 1…10)